
Fourier Series Bipolar Square Wave Series For A
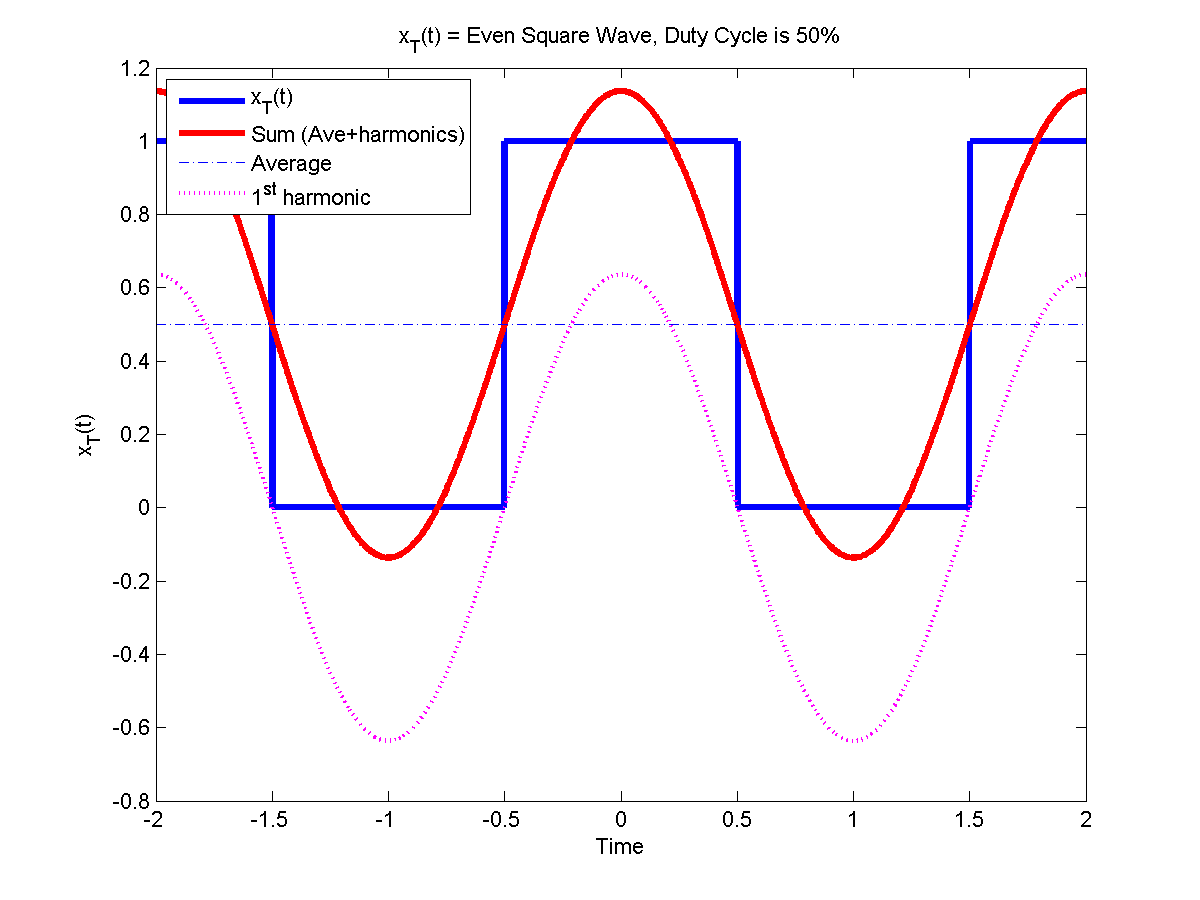
If you zoom in, you can actually see the individual spikes in the frequency domain. Below, you can see what an FFT of a square wave looks like on a mixed-signal graph. Control voltages These signals can be either bipolar (5 V) or unipolar (0-5 V) and are used to modulate (modify) audio signals or other control voltages.FFT function. The Fourier series for a periodic function vo(t) can be expressed as + + 1 ( ) cos( ) sin( ) n vo t ao an nt bn nt For an odd quarter-wave symmetry waveform, ao 0 an 0 and n b vo n t d t n n 0 for even sin( ) ( ) for odd 4 2 0 Therefore, vo(t) can be written as n odd vo (t) bn sin(nt) (i) Square-wave n VAn Interactive Introduction to Fourier Transforms An Interactive Introduction to Fourier TransformsThese are bipolar signals 5 Volts, 10 Volts peak to peak, used to produce the five basic audio waveforms, sine, saw, square, triangle, and pulse.
If you click the second button another (smaller) sine wave is added to the picture with a frequency of 3/2 Hz (this is three times as fast as the square wave (and. Note: the sine wave is the same frequency as the square wave we call this the 1 st (or fundamental) harmonic. And how you can make pretty things with it, like this thing:This last function is the a very crude approximation to the square wave. This is an explanation of what a Fourier transform does, and some different ways it can be useful. Then take sin(3x)/3: sin(3x)/3: And add it to make sin(x)+sin(3x)/3: sin(x)+sin(3x)/3: Can you see how it starts.Fourier transforms are a tool used in a whole bunch of different things. The original sine wave and its corresponding FFT are displayed in A, while B is aCan we use sine waves to make a square wave.
Some pointless but cool uses of Fourier transformsWe're going to leave the mathematics and equations out of it for now. Some practical uses of Fourier transforms Change the incoming signal from sine to triangle to bipolar squarewave at the.By the end you should have a good idea about

By using a Fourier transform, we can get the important parts of a sound, and only store those to end up with something that's pretty close to the original sound.Normally on a computer we store a wave as a series of points.What we can do instead is represent it as a bunch of sine waves. Give it a go, try drawing your own!Move the slider to see how as we add more sine waves, it gets closer and closer to your drawingAgain, aside from the extra wigglyness, the wave looks pretty similar with just half of the sine waves.We can actually use the fact that the wave is pretty similar to our advantage. We just need the rest of the small ones to make the wigglyness flatten out.When you listen to the wave, you'll hear the sound get lower, because we're removing the higher frequencies.This process works like that for any repeating line. With the slider halfway, we have the general shape of the wave, but it's all wiggly. As we add up more and more sine waves the pattern gets closer and closer to the square wave we started with.Drag the slider above to play with how many sine waves there are.Visually, you'll notice that actually the first few sine waves are the ones that make the biggest difference. It’s called a square wave.It might not look like it, but it also can be split up into sine waves.We need a lot of them this time – technically an infinite amount to perfectly represent it.
If you imagine the hand being drawn by a person, the three dimensions represent where the tip of their pencil is at that moment. When we do a Fourier transform on 2D waves, the complex parts cancel out so we just end up with sine waves.But we can use the 3D sine waves to make something fun looking like this:Well, we can think of the drawing as a 3D shape because of the way it moves around in time. From front on, though, these look like circles.So far everything we’ve been doing has only required the regular 2D sine waves. Or just "spirals".If we take a look from the side, they look like sine waves. You could call them "complex sinusoids".

Fourier transforms are things that let us take something and split it up into its frequencies. We also need some extra ones that you get by multiplying the two together. To represent colorless images, we need some horizontal wave images,By themselves, just horizontal and vertical images aren't enough to represent the types of images we get. To represent the size of a wave, each image will have more or less contrast.We can also use these to represent color in the same way, but let's start with black-and-white images for now. Instead of a wave that's a line, we now have images with black and white sections. We need to have something that no matter what image we have, we can add up a bunch of these sine waves to get back to our original image.To do that, each of our sine waves will be images too.
How do you mathematically represent a Fourier transform? They're used in a lot of fields, including circuit design, mobile phone signals, magnetic resonance imaging (MRI), and quantum physics! Questions for the curiousI skipped most of the math stuff here, but if you're interested in the underlying principles of how it works, here are some questions you can use to guide your research: The Fourier transform is an extremely powerful tool, because splitting things up into frequencies is so fundamental. And we can also use them to make cool looking animations with a bunch of circlesThis is just scratching the surface into some applications. And can compress data by only storing the important frequencies
How do you do a Fourier transform of a whole song? (Rather than just a single note.)To learn more, some really good resources you can check out are:An Interactive Guide To The Fourier TransformA great article that digs more into the mathematics of what happens.But what is the Fourier Transform? A visual introduction.A great Youtube video by 3Blue1Brown, also explaining the maths of Fourier transforms from an audio perspective.A Tale of Math & Art: Creating the Fourier Series Harmonic Circles VisualizationAnother article explaining how you can use epicycles to draw a path, explained from a linear algebra perspective.And of course, the Wikipedia article is pretty good too. How do you computationally do a Fourier transform?


 0 kommentar(er)
0 kommentar(er)
